Parallel Analysis
PA.RdThis function performs Parallel Analysis (PA), which is a method used to determine the number of factors to retain in exploratory factor analysis. It compares the empirical eigenvalues with those obtained from simulated random data to identify the point where the observed eigenvalues are larger than those expected by chance. The number of empirical eigenvalues that are greater than the corresponding reference eigenvalues is the number of factors recommended to be retained by the PA method.
PA(
response,
fa = "pc",
n.iter = 100,
type = "quant",
nfact = 1,
quant = 0.95,
cor.type = "pearson",
use = "pairwise.complete.obs",
vis = TRUE,
plot = TRUE
)Arguments
- response
A required
N×Imatrix or data.frame consisting of the responses ofNindividuals toIitems.- fa
A string that determines the method used to obtain eigenvalues in PA. If
"pc", it represents Principal Component Analysis (PCA); if"fa", it represents Principal Axis Factoring (a widely used Factor Analysis method; @seealsofactor.analysis; Auerswald & Moshagen, 2019). (Default ="pc")- n.iter
A numeric value that determines the number of simulations for the random data. (Default = 100)
- type
A string that determines the method used to calculate the reference eigenvalues from the simulated data. If
'mean', the reference eigenvalue (eigen.ref) is the mean of the simulated eigenvalues (eigen.sim); if'quant', the reference eigenvalue is thequantpercentile ofeigen.sim. (Default ='quant')- nfact
A numeric value that specifies the number of factors to extract, only effective when
fa = 'fa'. (Default = 1)- quant
A numeric value between 0 and 1, representing the quantile to be used for the reference eigenvalues calculation when
type = 'quant'. (Default = 0.95)- cor.type
A character string indicating which correlation coefficient (or covariance) is to be computed. One of
"pearson"(default),"kendall", or"spearman". @seealsocor.- use
an optional character string giving a method for computing covariances in the presence of missing values. This must be one of the strings
"everything","all.obs","complete.obs","na.or.complete", or"pairwise.complete.obs"(default). @seealsocor.- vis
A Boolean variable that will print the factor retention results when set to
TRUE, and will not print when set toFALSE. (default =TRUE)- plot
A Boolean variable that will print the PA plot when set to
TRUE, and will not print it when set toFALSE. @seealsoplot.PA. (Default =TRUE)
Value
An object of class PA, which is a list containing the following components:
- nfact
The number of factors to retain.
- fa
Indicates the method used to obtain eigenvalues in PA. 'pc' represents Principal Component Analysis, and 'fa' represents Principal Axis Factoring.
- type
Indicates the method used to calculate
eigen.ref. If 'mean',eigen.refis the mean ofeigen.sim; if 'quant',eigen.refis thequantpercentile ofeigen.sim.- eigen.value
A vector containing the empirical eigenvalues.
- eigen.ref
A vector containing the reference eigenvalues, which depend on
type.- eigen.sim
A matrix containing the simulated eigenvalues for all iterations.
Details
This function performs Parallel Analysis (PA; Horn, 1965; Auerswald & Moshagen, 2019) to determine the number of factors to retain. PA is a widely used method and is considered the "gold standard" for factor retention due to its high accuracy and stability, although it may underperform compared to methods like CD or EKC under certain conditions. The core idea of PA is to simulate random data multiple times, for example, 100 times, and compute the eigenvalues from each simulation. These simulated eigenvalues are then processed using either the mean or a quantile method to obtain the reference eigenvalues, such as the i-th reference eigenvalue \(\lambda_{i,ref}\). The relationship between the i-th empirical eigenvalue \(\lambda_{i}\) and \(\lambda_{i,ref}\) indicates whether the i-th factor should be retained. If \(\lambda_{i} > \lambda_{i,ref}\), it suggests that the explanatory power of the i-th factor from the original data is stronger than that of the i-th factor from the random data, and therefore the factor should be retained. Conversely, if \(\lambda_{i} <= \lambda_{i,ref}\), it indicates that the explanatory power of the i-th factor from the original data is weaker or equal to that of the random data, making it indistinguishable from noise, and thus the factor should not be retained. So,
$$F = \sum_{i=1}^{I} I(\lambda_i > \lambda_{i,ref})$$
Here, \( F \) represents the number of factors determined by the EKC, and \(I(\cdot)\) is the indicator function, which equals 1 when the condition is true, and 0 otherwise.
Auerswald & Moshagen (2019) found that the most accurate results for PA were obtained when
using PCA to extract eigenvalues and using the 95th percentile of the simulated
eigenvalues to calculate the reference eigenvalues. Therefore,
the recommended settings for this function are fa = 'pc', type = 'quant', and quant = 0.95.
References
Auerswald, M., & Moshagen, M. (2019). How to determine the number of factors to retain in exploratory factor analysis: A comparison of extraction methods under realistic conditions. Psychological methods, 24(4), 468-491. https://doi.org/10.1037/met0000200.
Horn, J. L. (1965). A rationale and test for the number of factors in factor analysis. Psychometrika, 30, 179–185. http://dx.doi.org/10.1007/BF02289447.
Examples
library(EFAfactors)
set.seed(123)
##Take the data.bfi dataset as an example.
data(data.bfi)
response <- as.matrix(data.bfi[, 1:25]) ## loading data
response <- na.omit(response) ## Remove samples with NA/missing values
## Transform the scores of reverse-scored items to normal scoring
response[, c(1, 9, 10, 11, 12, 22, 25)] <- 6 - response[, c(1, 9, 10, 11, 12, 22, 25)] + 1
## Run PA function with default parameters.
# \donttest{
PA.obj <- PA(response)
#> The number of factors suggested by PA (quant=0.95) is 5 .
 print(PA.obj)
#> The number of factors suggested by PA (quant=0.95) is 5 .
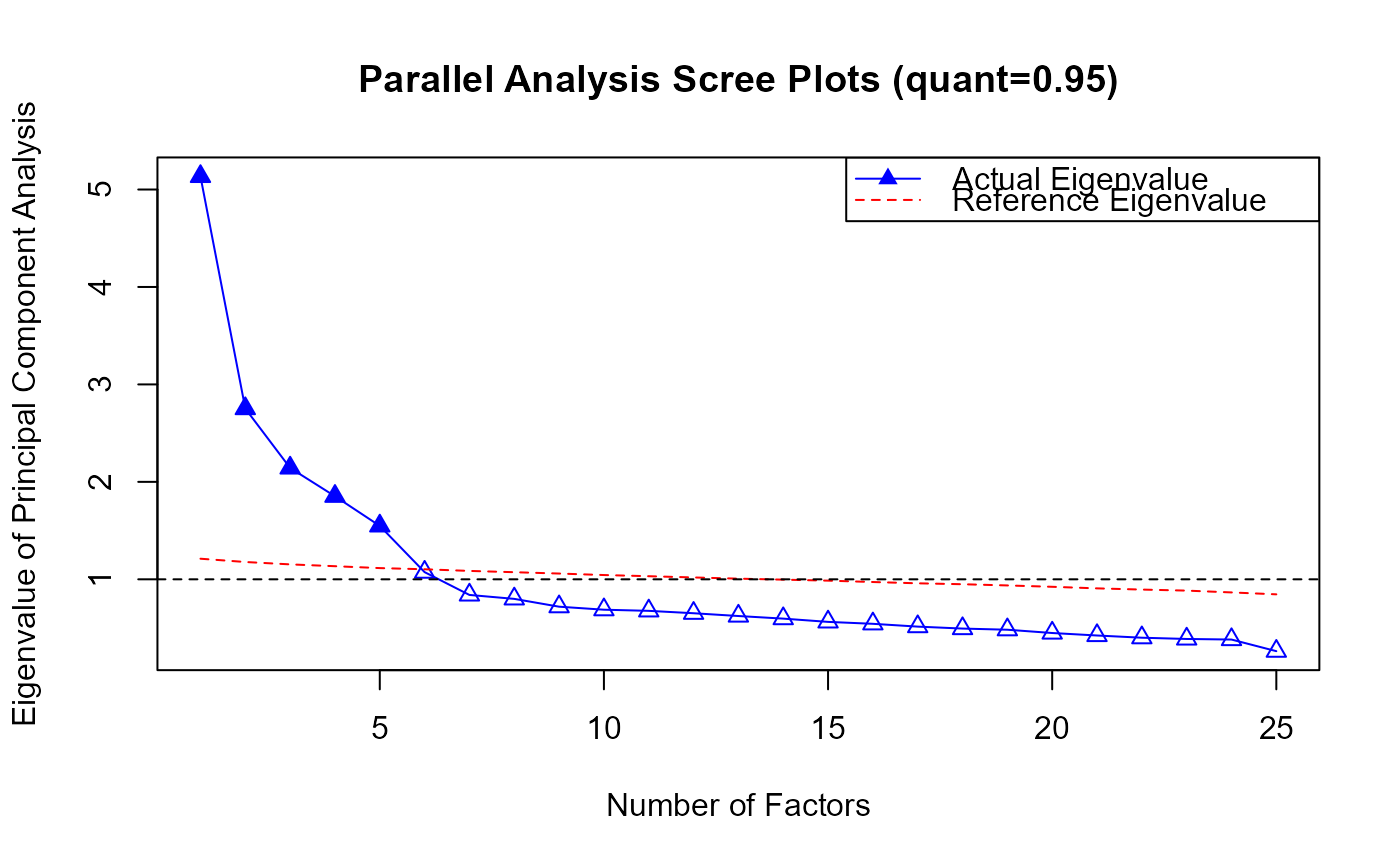
plot(PA.obj)
## Get the eigen.value, eigen.ref and nfact results.
eigen.value <- PA.obj$eigen.value
eigen.ref <- PA.obj$eigen.ref
nfact <- PA.obj$nfact
print(eigen.value)
#> [1] 5.1343112 2.7518867 2.1427020 1.8523276 1.5481628 1.0735825 0.8395389
#> [8] 0.7992062 0.7189892 0.6880888 0.6763734 0.6517998 0.6232530 0.5965628
#> [15] 0.5630908 0.5433053 0.5145175 0.4945031 0.4826395 0.4489210 0.4233661
#> [22] 0.4006715 0.3878045 0.3818568 0.2625390
print(eigen.ref)
#> [1] 1.2112834 1.1776117 1.1531890 1.1344426 1.1150697 1.1029669 1.0860779
#> [8] 1.0729105 1.0591319 1.0437886 1.0317484 1.0190511 1.0066855 0.9964805
#> [15] 0.9862649 0.9721713 0.9589159 0.9494823 0.9370774 0.9231573 0.9069998
#> [22] 0.8946235 0.8839700 0.8653672 0.8457528
print(nfact)
#> [1] 5
# }
print(PA.obj)
#> The number of factors suggested by PA (quant=0.95) is 5 .
plot(PA.obj)
## Get the eigen.value, eigen.ref and nfact results.
eigen.value <- PA.obj$eigen.value
eigen.ref <- PA.obj$eigen.ref
nfact <- PA.obj$nfact
print(eigen.value)
#> [1] 5.1343112 2.7518867 2.1427020 1.8523276 1.5481628 1.0735825 0.8395389
#> [8] 0.7992062 0.7189892 0.6880888 0.6763734 0.6517998 0.6232530 0.5965628
#> [15] 0.5630908 0.5433053 0.5145175 0.4945031 0.4826395 0.4489210 0.4233661
#> [22] 0.4006715 0.3878045 0.3818568 0.2625390
print(eigen.ref)
#> [1] 1.2112834 1.1776117 1.1531890 1.1344426 1.1150697 1.1029669 1.0860779
#> [8] 1.0729105 1.0591319 1.0437886 1.0317484 1.0190511 1.0066855 0.9964805
#> [15] 0.9862649 0.9721713 0.9589159 0.9494823 0.9370774 0.9231573 0.9069998
#> [22] 0.8946235 0.8839700 0.8653672 0.8457528
print(nfact)
#> [1] 5
# }