Hierarchical Clustering for EFA

A function performs clustering on items by calling hclust. Hierarchical cluster analysis on a set of dissimilarities and methods for analyzing it. The items will be continuously clustered in pairs until all items are grouped into a single cluster, at which point the process will stop.

EFAhclust(
  response,
  dissimilarity.type = "R",
  method = "ward.D",
  cor.type = "pearson",
  use = "pairwise.complete.obs",
  nfact.max = 10,
  plot = TRUE
)

Arguments

response

A required N × I matrix or data.frame consisting of the responses of N individuals to I items.

dissimilarity.type

A character indicating which kind of dissimilarity is to be computed. One of "R" or "E" (default) for the correlation coefficient or Euclidean distance.

method

the agglomeration method to be used. This should be (an unambiguous abbreviation of) one of "ward.D", "ward.D2", "single", "complete", "average" (= UPGMA), "mcquitty" (= WPGMA), "median" (= WPGMC) or "centroid" (= UPGMC). (default = "ward.D") @seealso hclust

cor.type

A character string indicating which correlation coefficient (or covariance) is to be computed. One of "pearson" (default), "kendall", or "spearman". @seealso cor.

use

An optional character string giving a method for computing covariances in the presence of missing values. This must be one of the strings "everything", "all.obs", "complete.obs", "na.or.complete", or "pairwise.complete.obs" (default). @seealso cor.

nfact.max

The maximum number of factors discussed by the Second-Order Difference (SOD) approach. (default = 10)

plot

A Boolean variable that will print the EFAhclust plot when set to TRUE, and will not print it when set to FALSE. @seealso plot.EFAhclust. (Default = TRUE)

Value

An object of class EFAhclust is a list containing the following components:

hc

An object of class hclust that describes the tree produced by the clustering process. @seealso hclust

cor.response

A matrix of dimension I × I containing all the correlation coefficients of items.

clusters

A list containing all the clusters.

heights

A vector containing all the heights of the cluster tree. The heights are arranged in descending order.

nfact.SOD

The number of factors to be retained by the Second-Order Difference (SOD) approach.

Details

Hierarchical cluster analysis always merges the two nodes with the smallest dissimilarity, forming a new node in the process. This continues until all nodes are merged into one large node, at which point the algorithm terminates. This method undoubtedly creates a hierarchical structure by the end of the process, which encompasses the relationships between all items: items with high correlation have short connecting lines between them, while items with low correlation have longer lines. This hierarchical structure is well-suited to be represented as a binary tree. In this representation, the dissimilarity between two nodes can be indicated by the height of the tree nodes; the greater the difference between nodes, the higher the height of the tree nodes connecting them (the longer the line). Researchers can decide whether two nodes belong to the same cluster based on the height differences between nodes, which, in exploratory factor analysis, represents whether these two nodes belong to the same latent factor.

The Second-Order Difference (SOD) approach is a commonly used method for finding the "elbow" (the point of greatest slope change). According to the principles of exploratory factor analysis, items belonging to different latent factors have lower correlations, while items under the same factor are more highly correlated. In hierarchical clustering, this is reflected in the height of the nodes in the dendrogram, with differences in node heights representing the relationships between items. By sorting all node heights in descending order and applying the SOD method to locate the elbow, the number of factors can be determined. @seealso EFAkmeans

References

Batagelj, V. (1988). Generalized Ward and Related Clustering Problems. In H. H. Bock, Classification and Related Methods of Data Analysis the First Conference of the International Federation of Classification Societies (IFCS), Amsterdam.

Murtagh, F., & Legendre, P. (2014). Ward’s Hierarchical Agglomerative Clustering Method: Which Algorithms Implement Ward’s Criterion? Journal of Classification, 31(3), 274-295. https://doi.org/10.1007/s00357-014-9161-z.

Examples

library(EFAfactors)
set.seed(123)

##Take the data.bfi dataset as an example.
data(data.bfi)

response <- as.matrix(data.bfi[, 1:25]) ## loading data
response <- na.omit(response) ## Remove samples with NA/missing values

## Transform the scores of reverse-scored items to normal scoring
response[, c(1, 9, 10, 11, 12, 22, 25)] <- 6 - response[, c(1, 9, 10, 11, 12, 22, 25)] + 1


## Run EFAhclust function with default parameters.
# \donttest{
 EFAhclust.obj <- EFAhclust(response)

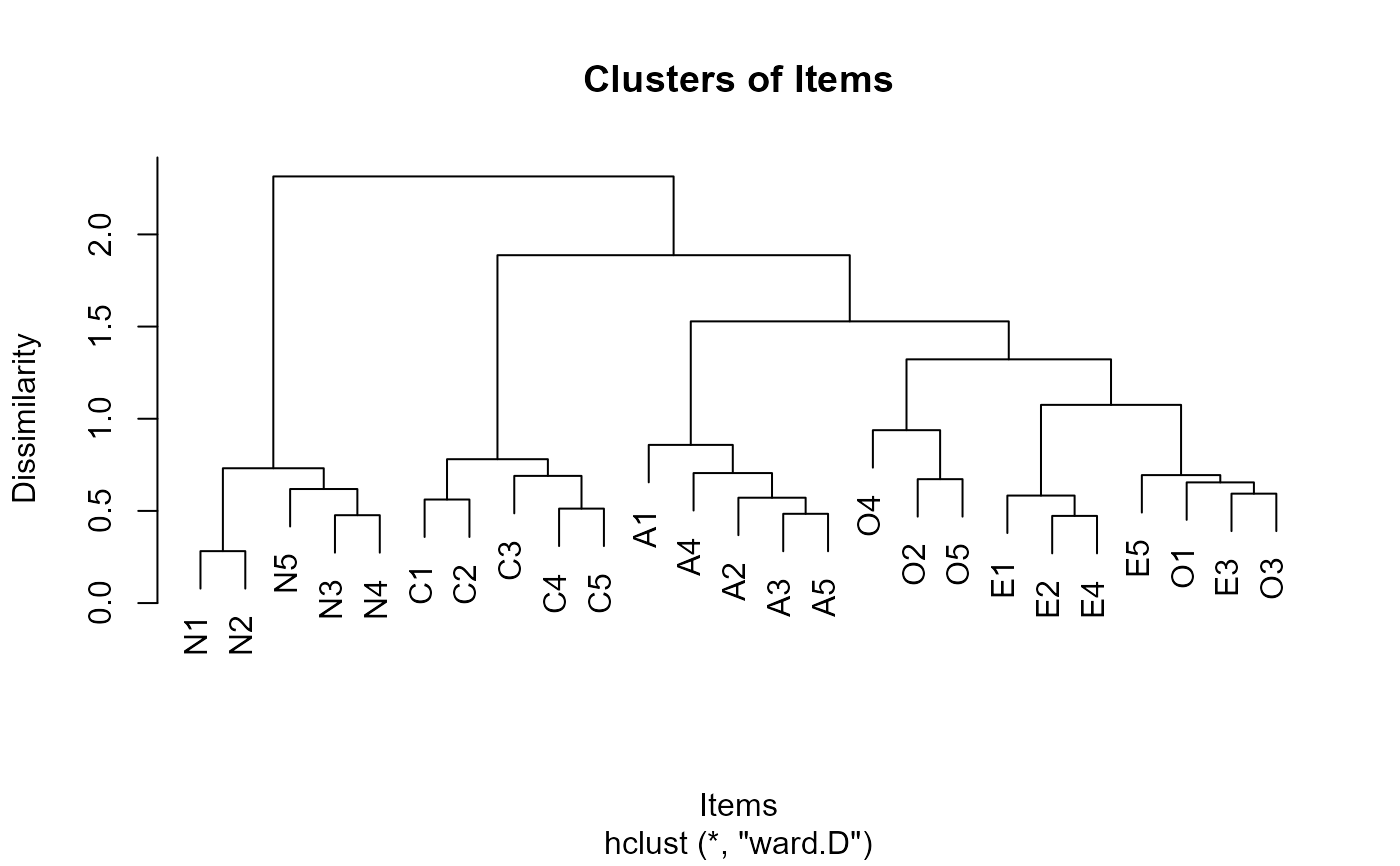 plot(EFAhclust.obj)


 ## Get the heights.
 heights <- EFAhclust.obj$heights
 print(heights)
#>  [1] 2.3145393 1.8872270 1.5282353 1.3222598 1.0753015 0.9379722 0.8581567
#>  [8] 0.7805235 0.7313742 0.7053110 0.6942536 0.6900018 0.6722169 0.6547298
#> [15] 0.6187218 0.5936228 0.5832322 0.5715987 0.5617770 0.5124492 0.4843213
#> [22] 0.4767299 0.4729118 0.2817402

 ## Get the nfact retained by SOD
 nfact.SOD <- EFAhclust.obj$nfact.SOD
 print(nfact.SOD)
#> [1] 3


# }