Kaiser-Guttman Criterion

This function implements the Kaiser-Guttman criterion (Guttman, 1954; Kaiser, 1960) for determining the number of factors to retain in factor analysis. It is based on the eigenvalues of the correlation matrix of the responses. According to the criterion, factors are retained if their corresponding eigenvalues are greater than 1.

KGC(
  response,
  fa = "pc",
  nfact = 1,
  cor.type = "pearson",
  use = "pairwise.complete.obs",
  vis = TRUE,
  plot = TRUE
)

Arguments

response

A required N × I matrix or data.frame consisting of the responses of N individuals to I items.

fa

A string that determines the method used to obtain eigenvalues. If 'pc', it represents Principal Component Analysis (PCA); if 'fa', it represents Principal Axis Factoring (a widely used Factor Analysis method; @seealso factor.analysis; Auerswald & Moshagen, 2019). (Default = 'pc')

nfact

A numeric value that specifies the number of factors to extract, only effective when fa = 'fa'. (Default = 1)

cor.type

A character string indicating which correlation coefficient (or covariance) is to be computed. One of "pearson" (default), "kendall", or "spearman". @seealso cor.

use

An optional character string giving a method for computing covariances in the presence of missing values. This must be one of the strings "everything", "all.obs", "complete.obs", "na.or.complete", or "pairwise.complete.obs" (default). @seealso cor.

vis

A Boolean variable that will print the factor retention results when set to TRUE, and will not print when set to FALSE. (default = TRUE)

plot

A Boolean variable that will print the KGC plot when set to TRUE, and will not print it when set to FALSE. @seealso plot.KGC. (Default = TRUE)

Value

An object of class KGC is a list containing the following components:

nfact

The number of factors to be retained.

eigen.value

A vector containing the empirical eigenvalues

References

Guttman, L. (1954). Some necessary conditions for common-factor analysis. Psychometrika, 19, 149–161. http://dx.doi.org/10.1007/BF02289162.

Kaiser, H. F. (1960). The application of electronic computers to factor analysis. Educational and Psychological Measurement, 20, 141–151. http://dx.doi.org/10.1177/001316446002000116.

Examples

library(EFAfactors)
set.seed(123)

##Take the data.bfi dataset as an example.
data(data.bfi)

response <- as.matrix(data.bfi[, 1:25]) ## loading data
response <- na.omit(response) ## Remove samples with NA/missing values

## Transform the scores of reverse-scored items to normal scoring
response[, c(1, 9, 10, 11, 12, 22, 25)] <- 6 - response[, c(1, 9, 10, 11, 12, 22, 25)] + 1


## Run KGC function with default parameters.
# \donttest{
 KGC.obj <- KGC(response)
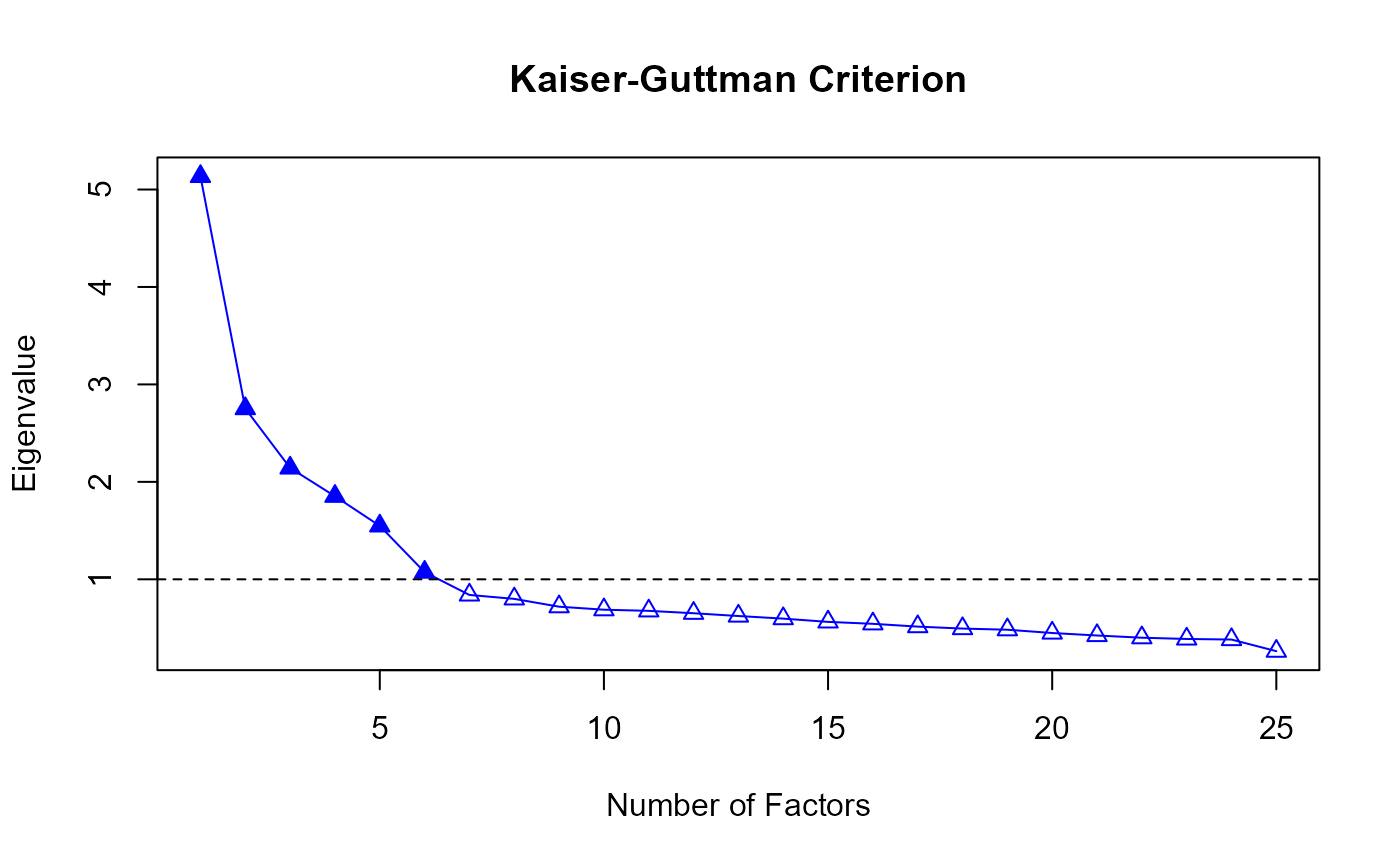#> The number of factors suggested by KGC is 6 .

 print(KGC.obj)
#> The number of factors suggested by KGC is 6 .

 plot(KGC.obj)


 ## Get the eigen.value, eigen.ref and  nfact results.
 eigen.value <- KGC.obj$eigen.value
 nfact <- KGC.obj$nfact

 print(eigen.value)
#>  [1] 5.1343112 2.7518867 2.1427020 1.8523276 1.5481628 1.0735825 0.8395389
#>  [8] 0.7992062 0.7189892 0.6880888 0.6763734 0.6517998 0.6232530 0.5965628
#> [15] 0.5630908 0.5433053 0.5145175 0.4945031 0.4826395 0.4489210 0.4233661
#> [22] 0.4006715 0.3878045 0.3818568 0.2625390
 print(nfact)
#> [1] 6

# }